Linear Algebra with apples, oranges and pineapples

To Understand Linear Algebra, let us make up a small day to day scenario.

Consider Surya goes to market every day and buys fruits. Surya went for past consecutive three days. Every day Surya bought apples, oranges and pineapples. Surya remembers the total cost that incurred but does not remembers what was the cost of 1 apple, 1 orange and 1 pineapple the seller sold.

Here are the 3 empirical outcomes, since it is consecutive three days, the fruits price might not have varied much, let us have it this way.

1.  3 apples, 2 oranges and 4 pineapple costed 270

2.  2 apples, 5 oranges and 3 pineapple costed 230

3.  6 apples, 3 oranges and 1 pineapple costed 250

and now Surya has to find out cost of 1 apple, 1 orange and 1 pineapple?  That is when Surya try to solve these above equations.

we can form a equation as below.

[ 3, 3, 4, 580

2, 5, 3, 420

6, 3 1 , 200]

what we want is (below given is not exact figures or exact solution)

[1, 0, 0, 40   => implies 1 apple = 30 bugs

0,1, 0, 10     => implies 1 orange = 10 bugs

0, 0, 1, 25]   => implies 1 pineapple = 40 bugs

So, you can see, What we always want is the diagonal matrix which is the solution to the given linear equations. Also see that what we mostly prefer is Identity Matrix. Reaching this diagonal matrix is not easily possible. so we go for first creating zeros in low triangular and then in the upper triangular. By scaling individual equations or by adding/subtracting  2 linear equations or by performing both.

These kind of calculation we must have performed in our schools as well, solving simultaneous linear equations.

apples, oranges and pineapples are dimensions, 3 dimension can be given with examples, consider 100s of dimensions what we will deal at work.

For 3 variables/dimensions, we definitely require 3 equations with all three variables involved in forming equation.

For n variables/dimensions, we definitely require n equations with all three variables involved in forming equation. Unless there are equations which involves less than n variables.

Can the diagonal element be zero?

For a matrix to be upper triangular or lower triangular matrix, zero in the diagonal does not matter, but for matrix to have a solution there should not be any zero in the diagonal. Zero in the diagonal means, Determinant of the matrix is zero. Zero in the diagonal means matrix inverse cannot be found since it is equal to adjunct of matrix divided by determinant.

What are Determinant and Adjacent?

Our objective is to convert a given system of linear equation into matrix and then into an Identity matrix to get the solution. How will we do this?

If we restate the same. we want all elements to be zero except for diagonal.

Consider this, does the below statement make a difference? 

 3 apples, 2 oranges and 4 pineapple cost 270

 2 oranges, 4 pineapple and 3 apples cost 270

As for the particular equation is concerned they are the same, the order of counting cost does not matter to find the total cost.

When we have system of equations, We have to shift the entire column, not just, the one element in the column. Because we want to compare apples to apples and do some manipulations like addition, subtraction.

Can I switch 2 equations? Will moving an equation above & below make any difference?

Does the order of days when Surya went to market matters? No. Hence order of equation also does not matters.

So, we are given with these 2 freedom of movements/rearranging the matrix.

1. equation switch

2. dimension switch

I have just given row & column switch/interchange a different meaningful names.

The above 2 freedom of movement did not do anything to the matrix, even to the numbers in the matrix. It just shuffles.

Consider this, will doubling the fruit count, double the total? Yes.

[3 apples, 2 oranges and 4 pineapple costed 270] then [6 apples, 4 oranges and 8 pineapples must be costing 540]. 

We have just multiplied the equation with 2, it could be any number other than 2. While doing so we see that we do not Touch the Other equations.

we can add and subtract two equations, given that we do the operation on co-efficient of same dimension and the operation is also done on corresponding cost.

There are 2 freedom of manipulations of equations

1. Addition/Subtraction between 2 equation.

2. Multiplication/Division of an equation by constant factor.

Can't we make a Commodity Exchange? Replace Apple with equivalent costing Oranges?

We can do it, but we have to do it simultaneously in all equations, not in only one equation as we really do not know the cost of each yet,. While doing so we see that we do not Touch the Total Cost.

we can add and subtract two commodities/dimension as well, given that we do the operation on co-efficient of different dimension.

There are 2 freedom of manipulations of dimensions

1. Addition/Subtraction between 2 commodities/dimension.

2. Multiplication/Division of commodities/dimension by constant factor.

The 6 freedom of moves that we could make on the game. They are the rules of game - THE MATRIX.

Can we treat the Total Cost also as a dimension/commodity? By that we question whether switch them and manipulate them along with other dimension/commodity allowed?

No, We should not, it is not a commodity or dimension. It is just a constant and not a variable co-efficient.

Now we know moves of each pieces on a Chess Board, sorry MATRIX ;)  we should now form a Strategy.

Our goal is to reach Identity Matrix, we can have sub goals. 

Either to attain LOWER triangular matrix first and the attain Identity Matrix or attain UPPER triangular matrix and the attain Identity Matrix. So Triangular Matrices are our Sub goals.

Sometimes, we attain only sub goal and the take the solution without attaining Identity Matrix via Substitution method.

There are few Strategies that have some special names,

1. Gauss Elimination Method & Substitution 

Attain first UPPER TRIANGULAR Matrix via freedom of movement and manipulations especially Row reduction. By now you could have got the cost of at least one commodity or dimension value. substitute them on other equations to get the cost of other commodities or dimension values.

What is Row reduction? - A reduction operation is an operation which reduces a number down to zero. If the reduction is done row wise, in this cases with manipulation between 2 equations. It is called row reduction.

If the reduction is done with columns/commodities/dimension it is called as column reduction.

2. Gauss Jordan Method 

Attain first UPPER TRIANGULAR Matrix by row reduction and then attain Identity matrix with column reduction.

All these Operations if we code in a program looks to be cost intensive, what if we want the solution straight forward?

That is when we require determinants and adjuncts or cofactors

Determinants takes its root from DETERMINE. 

Adjunct means a thing that is added or joined to something larger or more important. (small matrix of big matrix)

What determines the cost of Apples? 

The cost of Oranges and Pineapples determines the cost of Apples as the total cost is a CONSTANT value.

In Matrix, for each element in each equation has determinants they are called as MINORS. 

We do mining in these area to calculate adjunct and determinant and then to calculate A-1 (A inverse) for square matrix only. All we need is Identity A-1.A (A inverse matrix multiplied by A) is Identity I.

3x+2y=17

2x+3y=18

[3 2 17

2 3 18]

Determinant = 3x3 -2x2 = 5

Minor Matrix [3 -2

                        -2 3]

Adjunct or transpose of Minor Matrix = [3 -2

                                                                 -2 3]

A-1  = ( adjunct / det of matrix) = [ 3/5  -2/5

                                                     -2/5 3/5]

A-1 B = [ 3/5  -2/5   [ 17

             -2/5 3/5]         18]

           = [3

                4]

x =3, y =4

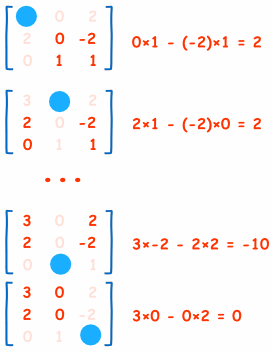
and get MATRIX of Minors.

These minors affect the actual via Co-factors.

By Transposing the Matrix of Co-factors we get Adjunct

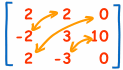
Cramer Rule goes one step further gives the solution directly with Determinants only

I felt little happy as Determinants alone is sufficient to get the solution, but it is not the case practically it seems.

Though Cramer's rule is important theoretically, it has little practical value for large matrices, since the computation of large determinants is somewhat cumbersome. (Indeed, large determinants are most easily computed using row reduction.) Further, Cramer's rule has very poor numerical properties, making it unsuitable for solving even small systems reliably, unless the operations are performed in rational arithmetic with unbounded precision.

References:

https://www.mathsisfun.com/algebra/matrix-inverse-minors-cofactors-adjugate.html

https://en.wikipedia.org/wiki/System_of_linear_equations

Mediation of a computer programmer

I don't have exact link from where i took the 1st 2 pictures but I did picture the 3rd one I took it while going through meme about python. I went through all 112 meditation techniques stated in Vigyan Bhairava Tantra. I have also done few dynamic meditations of Osho. The third image demonstrates nothing less all the different techniques of meditation. Despite the fact the first 2 images intimidates us with different technical terms and stages in meditation. Once you have attained Liberation, we have to come back to normal life. Please check this link and this link. Like Ox we should have Objective/Object in life and we should dissolve our self erasing everything else and finally the Objective/Object also dissolves leading us to Vanity.

My Review on "A Beginner’s Guide to Data Engineering - a 3 parts blog"

The main reason for the review is to summarize my takeaways from the blog.

The writer of the blog is a data scientist working in Airbnb and has also worked in Twitter. The blog is a writing of his understanding about his Adjacent field Data Engineering. I read many links provided in his blogs including his blogs on Data Science where he documents his work experience and also read an article about "Mastering Adjacent Disciplines".
His Main Objective for the blog was to document his learning of the Adjacent Disciplines.

Let me first summarize the points to take away in "Mastering Adjacent Disciplines"

1. First figure out what are your Adjacent discipline. Like the blogger, I am an aspirant data scientist, wanted to understand data engineering as an adjacent discipline. let us understand Adjacent discipline through examples and figure out what is it.

Product engineer, adjacent disciplines might include user interface design, user research, server development, or automated testing. 

For Infrastructure engineer, they might include database internals, basic web development, or machine learning. 

User growth engineers could benefit by increasing their skills in data science, marketing, behavioral psychology, and writing. 

For technical or project leads, adjacent disciplines might include both product management and people management. 

And if you’re a product manager or designer, you might learn to code.

2.  Understand the benefits to expend efforts

You will become self-sufficient and effective in your day-to-day job. 

Gives you the flexibility to potentially tackle those areas on your own. 

In comparison to learning a completely unrelated but perhaps still valuable discipline, you’re almost guaranteed to use these new skills you acquire in your day-to-day work. 

It benefits you and your team by increasing empathy of your team mates with other teams.

Let me also finish of with my takeaways from blog of the writer on Data Science.

1. We are not expected to be Unicorns, Unicorns do exists. I like to become one Unicorn.

Data science is not Teenage sex. i definitely know this. But we can't help people speaking about it like Teenage sex. They are just Marketing, Sales motivators but over-emphasizes real Data Scientist role and the need of Data Science.  

All DS need not be unicorns with expertise from Math/Stat, CS/ML/Algorithms, to data. We don't have such demands in the industry but Unicorns do exists.

2.  There are 2 types of Data Scientist. My skills and opportunities are almost of that of Type B, I had to move towards Type A to add more meaning to the domain of operation.

Type A Data Scientist: The A is for Analysis. This type is primarily concerned with making sense of data or working with it in a fairly static way. The Type A Data Scientist is very similar to a statistician (and may be one) but knows all the practical details of working with data that aren’t taught in the statistics curriculum: data cleaning, methods for dealing with very large data sets, visualization, deep knowledge of a particular domain, writing well about data, and so on.

Type B Data Scientist: The B is for Building. Type B Data Scientists share some statistical background with Type A, but they are also very strong coders and may be trained software engineers. The Type B Data Scientist is mainly interested in using data “in production.” They build models which interact with users, often serving recommendations (products, people you may know, ads, movies, search results).

3. Where to land for a Job and what will be the nature of work? I have taken the startup as "investigation start" on data and not as a startup company. All I had dream seem to fall only in scaled companies. I am currently under some early start up stage :(

At early stage start-ups: the primary analytic focus is to implement logging, to build ETL processes, to model data and design schemas so data can be tracked and stored. The goal here is focused on building the analytics foundation rather than analysis itself. 

At mid-stage growing start-ups: Since the company is growing, the data is probably growing too. The data platform needs to adapt, but with the foundation laid out already, there will be a natural shift to insight generation. Unless the company leverages Data Science for its strategic differentiation to start with, many analytics work are around defining KPI, attributing growth, and finding the next opportunities to grow. 

Companies who achieved scale: When the company scales up, data also scales up. It needs to leverage data to create or maintain competitive edge. e.g. Search results need to be better, recommendations need to be more relevant, logistics or operations need to be more efficient — this is the time where specialist like ML engineers, Optimization experts, Experimentation designers can play a huge role in stepping up the game. 

4. Understand the Job Nature as a whole. I am Nowhere near here. It is well taken, it is completely a different world. I shall move from Nowhere to Now here.

Skill that are required - Programming, Analytical and Experimentation.
Understanding of Infrastructure & Data pipelines - the Product, Instrument, Experiment, A/B test and Deploy

Hope that convinced you to read my blog further despite you being a data scientist aspirant just like me. Let me also put forth my take away with respect to "Data Engineering" blog.

1. Monica Rogati’s call out

Think of Artificial Intelligence as the top of a pyramid of needs. Yes, self-actualization (AI) is great, but you first need food, water, and shelter (data literacy, collection, and infrastructure).

 

2. Better understanding of "Data Engineering" field

The data engineering field could be thought of as a superset of business intelligence and data warehousing that brings more elements from software engineering. This discipline also integrates specialization around the operation of so called “big data” distributed systems, along with concepts around the extended Hadoop ecosystem, stream processing, and in computation at scale. 

A link reference from the writer blog led to The Rise of the Data Engineer. Where I could make better sense of Data Engineering field.

1. The need for flexible ETL tools lead to developement of new ETL tools like Airflow, Oozie, Azkabhan or Luigi.

2. Old ETL tools which had drag and drop facilities like Informatica, IBM Datastage, Cognos, AbInitio or Microsoft SSIS have become obsolete. 

3. New ETL tools provides flexibility and abstractions to maintain experiments, schedule experiments, allow A/B testing. They are more Open Systems.

4. Data modeling has changed - Much denormalization possiblities, better blob support, dynamic creation of schemas, snapshoting and conformane of dimensions of schemas have become less imperative. 

5. Datawarehouse is the gravity around which data engineering still moves around. Yet Datawarehouse is also publicly shared with Data Scientist & Analyst. It has become to much Centric to the IT organization as a whole, rather than Data Engineer being its owner.

6. Heavy performance tuning & optimization are being achieved as more money is invested to pour in more data and experiment with same resources. 

7. Data Integration from SAAS based OLTP applications have become difficult. Non Standard and Changing API of OLTP systems are disrupting OLAP system.

3. ETL Paradigms: JVM based ETLs and SQL based ETLs are two track of choice.

4. Understanding of Job Nature of "Data Engineer"

Build Data Warehouses with ETLs and managing data pipelines (DAG - Directed Acyclic graphs). 

Data modeling (Data Normalization and Star Schema), Data Partitioning and back filling historical records. Fact and Dimension Tables.

5. Understanding the need of moving from pipelines to frameworks.

Standalone pipelines to Dynamic pipelines have become need of the hour. It is now possible by constructing DAG via simple configuration files such yaml and has to deploy well known patterns as frameworks.

Incremental Computation Framework 

To avoid full table scans for aggregation functions, this framework pre-calculating them daily, monthly, quarterly and avoids them when data scientist does such operations.

Back fill Framework 

Back filling of historical or update records is a tedious job. But it will have to take frequently, such jobs are run with this framework. 

Global Metrics Framework

De-normalization Machines to make Dimensional cut based metrics to build de-normalized schema automatically as required for both data scientist and market facing business people

Experimentation Reporting Framework

Every data company builds experimental models in a modular fashion which remains very lengthy than production models. These most complex ETL jobs have to executed and statistical calculation are captured per module instead of complete workflow to make decisions. 

The Data Mining I did to Understand Data Mining

Why you should read this blog? What will be your takeaway?

1. Better Understanding of "Data Mining"
2. Picture data mining perfectly among the misty jargon
3. Helps to understand a student's journey.


It was my first Data Mining class of M.Tech in Data science. I was not completely focused during the class hour as the class lecture bewildered me to think What is Data Mining?

Is the word "Mining" in "Data Mining" Misleading?

I started looking for the difference between data science and data mining. My Initial though was that "Data Mining" is nothing but data collection. I thought so because, when i went through "Statistical Mathematics", the collection and cleaning of data for performing some analysis itself was huge task. Consider the age where there was no social media and no internet. Statistics had its birth out of mathematics especially probability theory. Census was very much important for proper governance during that era and people have to visit each household, each and every village and cities to collect data.  Consider every revolution any country had seen. At all these revolution huge of amount of data was required and people did collect from every required corner of the globe to bring in revolutions. So was my assumption that "Data Mining" is collection of data.

Black Revolution	Related with Petroleum Production
Blue Revolution	Related with Fish Production
Brown Revolution	Related with Leather, Cocoa
Golden Fibre Revolution	Related with Jute Production
Golden Revolution	Related with Overall Horticulture, Honey, Fruit Production
Green Revolution	Related with Agriculture Production
Grey Revolution	Related with Fertilizers
Pink Revolution	Related with Onions, Prawn
Red Revolution	Related with Meat, Tomato Production
Evergreen Revolution	Intended for overall agriculture production growth
Round Revolution	Related with Potato Production
Silver Fibre Revolution	Related with Cotton Production
Silver Revolution	Related with Egg Production
White Revolution	Related with Dairy, Milk Production
Yellow Revolution	Related with Oil Seed Production
Round Revolution	Related with Potato

Hopes turned despair and I was confused

More through the lecture my hopes were turning into disparity as the lecture took a direction different from "Data Collection". The course of the lecture was not anywhere near how to collect data, where to find for sources. How to select the sources. I started reading about the difference between Data Mining and Data Science. Instead of clearing my doubts, it catalyzed my already burning confusion.

Here is the site, I checked out .

I came across other names of "Data mining"
1. Data Archaeology
2. Data Discovery
3. Information Harvesting
4. Knowledge Extraction

Got confused and started thinking more in terms of Archaeology. Selecting site for digging after a long and thorough analysis of histories (like keeladi site excavation), theories and speculating few finding based on other findings in hand. Looks I am right, data mining seems to be data collection, but collection of data from rare sites and collection of Golden Nuggets among the debris.

With the term Data Discovery, I can say, Discovery of natural phenomenon have never been straight forward, 99.999999%, human just stumbled upon them. While "Need is mother of all Inventions", discovery unlike it has a bizzare path. Discovery has everything to do with Nature. One has to look into to Nature to discover as one is just finding what is there all the time, while invention is just a process of putting things together as per the need. Only once in a while someone discovers something meaningful in the era in which he discovers.

While thinking about Information harvesting, when did we sow the seeds to grow data to harvest?. Yes, we do sow the seeds via all our OLTP systems. Consider every form we fill to give our personal details or fill some events as part of job or fill workflow input data to generate events. Forms are our fields, input data are our seeds. Data grows in velocity, variety and volume to produce Information and we harvest Information.

While thinking about Knowledge Extraction, Knowledge is nothing but Connecting dots of Information.







None of the other names of "Data Mining" brought clarity. Data Mining, Data Archaeology and Data Discovery point a direction towards searching dirty data pile, while Knowledge discovery and Information Harvesting point out the act of extracting the Golden Nuggets.


Classify the data to get information, connect information to get knowledge. Exercising the knowledge at the required situation or context in a globally acceptable way is wisdom. Wisdom creates an impact. All is well. Yet what is data Mining?






Better Picture of the "Extraction of Golden Nuggets" Appeared

Given the confusion, i started searching for images and more clarification linking data science and data mining.









With the above images, I hit the jackpot. Everything fell into the singularity. With data science we seem to analyze the past to predict the future by penetrating the data via analysis, then analytics - automating analysis a bit with logic(completely analytical math), then with data mining - proactively making sense with heuristics with causation and correlation of different dimensional data.

The above stated comparison seems sufficient. I think we should never compare the data mining & tasks (mostly i see classification, regression etc.,) with storage systems like data lakes and data warehouses, techniques & tools like statistics methods or BI tools or Machine learning and  Roles like Data Engineer, Data Scientists,  Data Analyst, despite they are required while performing Data mining. Confusing roles, storage, technique and methods seems to be the cause of ill. At least I was receiving some information so and so during the lecture with my antenna.

Given the relief I shared one more link which I read to differentiate "Data lakes" and "Data Warehouses" with my class students - here it is.

To conclude, Data Mining is a Technique, focused on Business Process to extract Patterns of Information with the purpose of finding trends previously not found. In order to perform data mining, one has to have the understanding of data whereabouts in order to navigate across and its statistical understanding to conduct Mining operation. It is a part of Data Science to conduct Data Mining on Structured data while dealing with both structured and unstructured data. AI is part of Data Mining. There are 4 perspectives for AI. Only one winner which is what is required for Data science and the Winner is "AI which acts rationally and achieves result in optimal expense of resources (time & memory) while applying heuristics over data mine field. Machine learning and deep learning or anyway a part of AI and so they become part of Data Mining.







P.S - The lecture also expounded some business areas where data mining is applied but i was not able to appreciate them without proper understanding or definition of the term "Data Mining" itself. Hope I missed it or lecture never had it.

Feynmann Diagrams

Below are the two videos related to Feynman's diagram.

Paul Dirac out of despair writes down a little paper on Quantum Mechanics stating how in many possibilities that some particle interactions could happen.

It is this little paper which invites Feynman's attention to make the problem intuitive with Feynman's diagram.

In the below videos, I could clearly understand the diagram in relativity or space time Continuum.

It bound to works taking Space and time into consideration and particle, particle interactions and their combinations. What is more interesting is that how probability plays a role in figuring out what is dominant strategy of interaction or occurring most of the time and what is not dominant or occurring very less no. of times. This usage marks the practical applications of Quantum Mechanics or QED - Quantum Electrodynamics.

The Strong and Weak Nuclear forces which makes the world of Quantum Mechanics, Dynamics or Computing, for me looks to be attractive or repulsive forces with very less or more flux as in magnetism. I am not sure why there are 4 forces put apart separated out - Gravity, Electomagnetic, Strong Nuclear and Weak Nuclear. Can't we explain them with Biology or Life forces of plants, animal or solar systems or universe?

Believe Alignment and Magnetism generates Gravity

Prof  Eric Laithwaite, an england professor and marvelous engineer show his incredible work in the below videos. His engineering tactics are really marvelous, what impressed me was that, he was totally practical without any much of mathematics and theory, he tries out all faulty things and discovers good solution meticulously keep in mind the economy of the solution if implemented in large scale for public.

I stumble up on this video when I was trying to re-imagine gravity with magnetism, which was a constant intuition, as Gravity is the only component that does not fits in "Theory of Everything" or "Unification of forces". I happend to read "Theory of Universal Magnetism" which was propounded by Vedanthiri Maharishi and admired that this thought had not been anything new and I do know that in Hindu Literature and Yogic science, there is lot of talk about Aura and the flux energy of a person.

The "Universal Magnetism", tries to explain both about microcosm and the macrocosm with magnetic forces i.e., via bio magnets. It seems to explains wonderfully about how magnetism can help explain the universe. I had one disagreement which i am not clear what was it about while writing this blog. I remember that it has to do something with 5 elements, earth, fire, water, sky(akash) and air and how the flux energy should reside outside body as AURA, but somehow it was stated in an opposite sense that AURA remains within body.

I came across Laithwaite videos, while searching to understand Earth & Sun magnetic poles and their impact on each other and why planets and starts revolves.

Below are take away i consider post watching Laithwaite videos,

1. Creativity with Engine wingdings and models.

    a. how to change circular motion to linear motion

    b. how to change concentrated circular coils help sustain levitation.

2. Shape of things and how to obtain inspiration with a Tea Pot.

3. How one can explain other laws of nature like Boyle's law, thermodynamics with just magnetism.

4. How to think about economy of a Solution.

5. Loved his conclusion that Big Motors are efficient that Small Motors and how magnetism plays its role in both microcosm and macrocosm.

Laithwaite videos helped me to understand nature in terms of merging duality into one and witness the duality.

Linear motion and Electrical Waves

Motors Small & Large

Magnetism for explaining Gas flow & laws , Liquid and Gun

Change Shape, engineering tactics to Levitation & Linear Motion