Introduction to Special Matrices

My journey with Special Matrices started with Transpose Operation, you can read about it in this post as you could find few interesting ones already over there.

There are so many number of special matrices(named matrices), but we shall see few of them.

In the previous blog, we saw that Unitary Matrix U has property U^∗U = U^∗U  = I. I being Identity. 

In the previous blog, we saw that Orthogonal Matrix has property A^TA = AA^T = I, I being Identity. 

I found that few matrices are named as Normal Matrices. When A*A = AA* but need not be equal to I (identity matrix). Among complex matrices, all Unitary, Hermitian, and skew-Hermitian matrices are normal. Likewise, among real matrices, all orthogonal (A^TA = AA^T = I), symmetric (A^TA = AA^T), and skew-symmetric (A^TA = AA^T) matrices are normal. However, it is not the case that all normal matrices are either unitary or (skew-)Hermitian.

I found Symplectic matrix interesting as i found it to be related to Transpose and Skew-Symmetric Matrix. It is a Dual Combo.

Symplectic matrix is a 2n × 2n matrix M with real entries that satisfies the condition

where M^T denotes the transpose of M and Ω is a fixed 2n × 2n nonsingular, skew-symmetric matrix. 

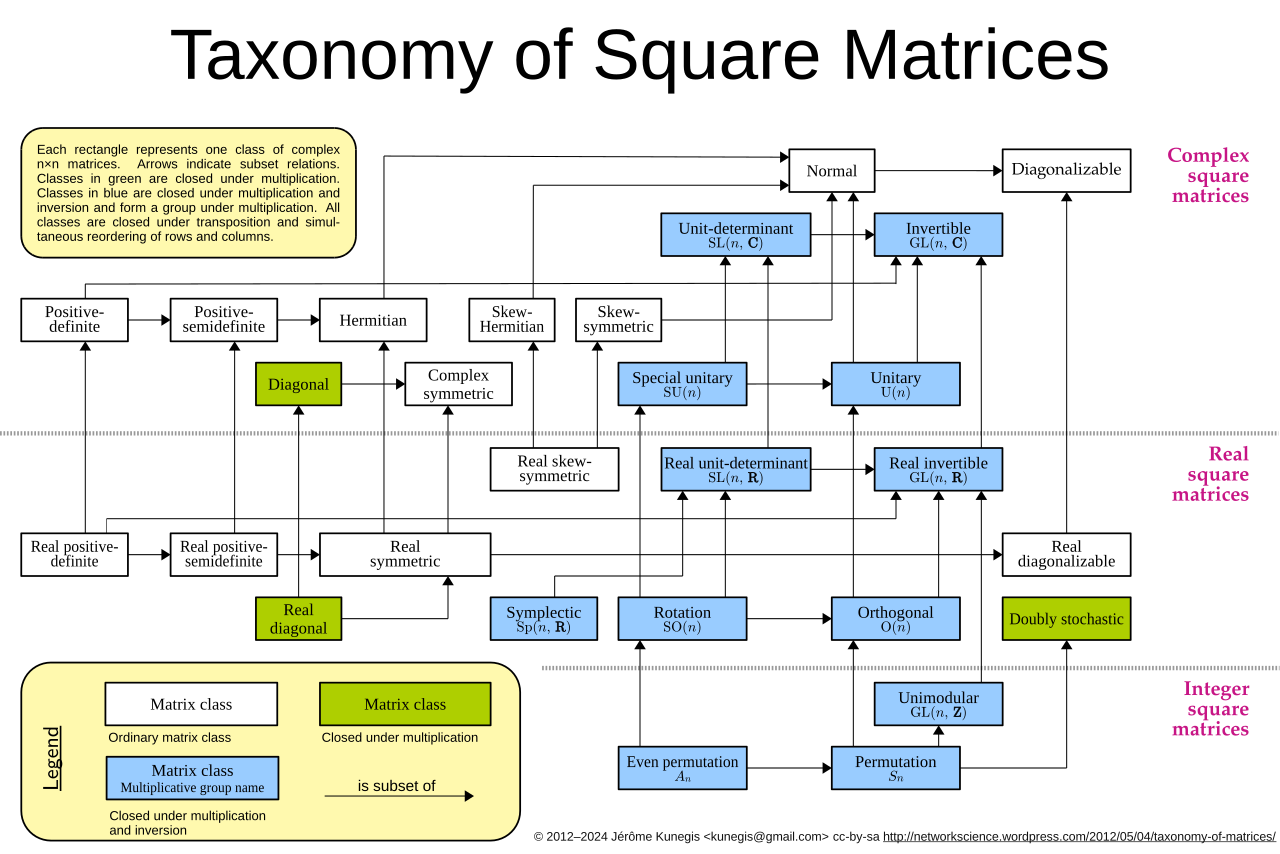
The below picture from wikipaedia, provides few named matrices and their relations. The wikipaedia page provides almost all present named matrices despite no relationship been identified. I have not gone through other interesting ones, may be they are for another blog.