Takeaways,
1. Determinant is nothing but a Common multiple factor or Scaling factor by which all the dimension have increased/reduced in its area, volume etc.,
2. Adjugate Matrix multiplication with Matrix is like Cross Multiplication.
3. Inverse of A is division by Common factor and Cross multiplication of transpose of co-factor Matrix of A.
4. Transpose of co-factors are only named as Adjugate - this naming is leading to all cause of confusion.
6. Theorems on Determinants.
|A| = det(A) ≠ 0. A matrix is said to be invertible, non-singular, or non–degenerative.
I tried to explain determinant and adjuncts, but was fairly unsuccessful with my previous blog. With this blog, i like to give a one more try.
I lost my flow, when i started explaining, minor, co-factors and failed to explain why determination is manipulated with minors and how the sign of co-factors play a role in the calculation towards the single value Determinant.
Blogging this stuff is not going to help my M.Tech in data science but will help to gain deeper insight to gain better intuition.
My Book for references is "Elementary Linear Algebra by Howard Anton / Chris Rorrers", I am sure google gave me this book as the best for learning linear algebra few months back.
It has a chapter for deteminants with 3 subsections.
1. Determinats by co-factor expansion.
2. Evaluating deteminant by Row Reduction.
3. Properties of Deteminants; Cramers Rule.
Few of my assumptions:
1. black box under study and the kernels
What is Black Box?
Consider a simple system of equations,
x+y+z = 25
2x+3y+4z = 120
5x+3y+z = 30
we can call x, y, z as 3 inputs, we don't know the exact system. The system to which we send the inputs was a black box. We got the output as 25. one of our empirical formula to describe black box is linear combination of all three inputs which is x+y+z. As far now the kernel of the system is x+y+z =25.
Similarly we have 2 more kernel of the same system 2x+3y+4z = 120 and 5x+3y+z = 30. With these three kernel, we try to determine actual system model.
Model is mathematical model, once we identify this, we know for any input of x, y, z what will be the value of b. That is we could calculate output of 4x+6y+7z. which we don't know.
Model is our Black Box.
What is kernel?
Kernel in these languages are nothing but seed. It has got all information about the plant, the plant could be a vegetable plant, fruit plant or a banyan tree, anything at all. We don't know we have to figure out.
Kernel is nothing but any f(x) function. Here we have 3 variable, so it is f(x,y,z), it maps to constant value some "b" as output. We don't know what is f function. But we know f(x,y,z) = b or AX=B as we assumed our system to be linear. X =(x,y,z) vector, A is the matrix f, as we don't deal with one kernel but 3. B is b, but it is a vector.
vector is nothing but a tuple, but it is a special tuple as it is formed from three independent observation or empirical outcomes and they are pointing the direction for us for finding actual model / black box.
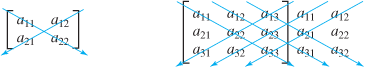
2. Minors are subsets, affecting factors of the unknown variables/inputs x, y, z
Minors are the one which affects the value of unknown variable (x or y or z) of selection? They are the affecting the unknown variable, so we measure what is the factor with which they affect.
Points to note with respect to minors,
3. The way Co-factors determined with minors can be +ve or -ve
it can be easily visualized, that there are +ve factors and -ve factors affecting the unknown.
[+ -
- +]

Factors are called as co-factors, as they come from different dimension. i.e., x is affected by y and z, y is affected by x and z etc.,
Vectors in the same direction affects +vely, and vectors in opposing direction affects -vely.
4. Why Adjunct is the transpose of Co-factor matrix?
Here is link questioning about the intuition of Adjunct.
https://math.stackexchange.com/questions/254774/what-is-the-intuitive-meaning-of-the-adjugate-matrix
1. Identity Matrix scaled by value of determinant is equal to Adj(A).A or A.Adj(A) is equals to I.Det(A) or Det(A).I
2. Adj(A) has same size or dimensions as A.
3. It is a natural pair of A.
It should exists for every invertible systems. i.e., x affecting y and z should be reversible. The impact should be translation and scaling only.
Adj(A) can be scaled by a common factor from A by 1/Det(A). if not scaled Det(A) is 1.
By Transpose, we change row to columns and columns to rows. When we balance the equations, we obvious multiply entire equation with common factor or cross multiply. We transpose Co-factor matrix and then multiply it Matrix A similar to Cross Multiply. Det(A) is the common factor, which is cancelled out post multiplication. We can also first divide by common factor and then cross multiply. If common factor is zero, there is no singular solution.
Like shown below,
To find 2/3 + 3/4, we multiply, first term with 4 and the second term with 3
(2*4) / (3*4) + (3*3)/(4*3) = 8/12 + 9/12
Now there is a common factor 12
So we can say
8/12 + 9/12 = (8+9)/12 = 17/12
Adj(A) is Transpose of Co-factor matrix.
Determinants says a lot of things about Matrices.
1. Says whether Matrix/system of equations is invertible or not.
By that, we question whether we can find x, y, z at all. A system has to be invertible if we have to determine it model with the help of inputs and outputs alone.
<To Include system and signals>
2. It deals with square matrix of all orders.
What are determinants?
Determinants are Tool to plots few points on graph
Determinant function is a tool to plot of more points on a graph, while we have already plotted few points saying these were empirical outcomes of the black box system.
Here det(A) is a number and A is a Matrix.
Quote from book,
Quote from book,
Determinants are Ratio of increase of the volume
There are lot of terms introduced in the below video like monte carlo integration, eigen values and eigen vectors, but the video completes with idea of determinants as below.
det(A) = increase volume / old volume
It confirms that that it is a scaling factor of all dimension. Whether it is scaling all dimension uniformly, is another question, you might wonder. Scaling may not be uniform, it could get skewed unless there are few characteristic vectors or eigen vectors.
If there are vectors that only stretch and don't change direction and their scaling is determined by some called as eigen values, then determinants can be easily expressed interms of eigen values over eigen vectors.
Determinants are Ratio of increase of the Area
In 3Blue1Brown channel, Determinant are stated as Ratio of increase of Area as they are not dealing with cube rather are dealing with 2x2 matrix and plane.
Geometrical Viewpoint of Vectors & Matrices
In almost in the entire play list, the matrices are treated as Vectors with origin at zero and the operation we do on vectors as Transformation, transformation can be like reflection, rotation, scaling over the basis etc., and the basis need not be co-ordinate system, rather i could be anything other than that, which is linearly translated or scaled. Any transformation taking place in basis also takes place on the entire system build on top of basis. Basis also determines the span of the system, i.e., all possible vectors on space given the basis.
Matrix is build with 2 or more vectors. Matrix multiplication is nothing but transformation on 2 or more vectors basis. It could be rotation, sheering or sometimes combination of both.
Inverse is nothing but reversal of the transformation to put back the basis vector in the place where it was present originally.
Basis vector is linearly dependent then its actual dimensions gets reduced and cannot be called as linearly independent or used for linear algebra.
Methods for Calculation of Determinants:
1. Cofactor Expansion
2. Condensation
References
https://www.ams.org/notices/199906/fea-bressoud.pdf
https://en.wikipedia.org/wiki/Dodgson_condensation
https://sms.math.nus.edu.sg/smsmedley/Vol-13-2/Some%20remarks%20on%20the%20history%20of%20linear%20algebra(CT%20Chong).pdf
https://docs.google.com/presentation/d/1qNj3lwCxLOELPfOIA735Phnr6fOp-v2Xk043pv3SHM0/edit#slide=id.p28
http://www.macs.citadel.edu/chenm/240.dir/12fal.dir/history2.pdf
http://courses.daiict.ac.in/pluginfile.php/15708/mod_resource/content/1/linear_algebra_History_Linear_Algebra.pdf
1. Determinant is nothing but a Common multiple factor or Scaling factor by which all the dimension have increased/reduced in its area, volume etc.,
2. Adjugate Matrix multiplication with Matrix is like Cross Multiplication.
3. Inverse of A is division by Common factor and Cross multiplication of transpose of co-factor Matrix of A.
4. Transpose of co-factors are only named as Adjugate - this naming is leading to all cause of confusion.
The use of the term adjoint for the transpose of the matrix of cofactors appears to have5. Ways to calculate Determinants.
been introduced by the American mathematician L. E. Dickson in a research paper that he published in 1902.
6. Theorems on Determinants.
|A| = det(A) ≠ 0. A matrix is said to be invertible, non-singular, or non–degenerative.
I tried to explain determinant and adjuncts, but was fairly unsuccessful with my previous blog. With this blog, i like to give a one more try.
I lost my flow, when i started explaining, minor, co-factors and failed to explain why determination is manipulated with minors and how the sign of co-factors play a role in the calculation towards the single value Determinant.
Blogging this stuff is not going to help my M.Tech in data science but will help to gain deeper insight to gain better intuition.
My Book for references is "Elementary Linear Algebra by Howard Anton / Chris Rorrers", I am sure google gave me this book as the best for learning linear algebra few months back.
It has a chapter for deteminants with 3 subsections.
1. Determinats by co-factor expansion.
2. Evaluating deteminant by Row Reduction.
3. Properties of Deteminants; Cramers Rule.
Few of my assumptions:
1. black box under study and the kernels
What is Black Box?
Consider a simple system of equations,
x+y+z = 25
2x+3y+4z = 120
5x+3y+z = 30
we can call x, y, z as 3 inputs, we don't know the exact system. The system to which we send the inputs was a black box. We got the output as 25. one of our empirical formula to describe black box is linear combination of all three inputs which is x+y+z. As far now the kernel of the system is x+y+z =25.
Similarly we have 2 more kernel of the same system 2x+3y+4z = 120 and 5x+3y+z = 30. With these three kernel, we try to determine actual system model.
Model is mathematical model, once we identify this, we know for any input of x, y, z what will be the value of b. That is we could calculate output of 4x+6y+7z. which we don't know.
Model is our Black Box.
What is kernel?
Kernel in these languages are nothing but seed. It has got all information about the plant, the plant could be a vegetable plant, fruit plant or a banyan tree, anything at all. We don't know we have to figure out.
Kernel is nothing but any f(x) function. Here we have 3 variable, so it is f(x,y,z), it maps to constant value some "b" as output. We don't know what is f function. But we know f(x,y,z) = b or AX=B as we assumed our system to be linear. X =(x,y,z) vector, A is the matrix f, as we don't deal with one kernel but 3. B is b, but it is a vector.
vector is nothing but a tuple, but it is a special tuple as it is formed from three independent observation or empirical outcomes and they are pointing the direction for us for finding actual model / black box.
2. Minors are subsets, affecting factors of the unknown variables/inputs x, y, z
Minors are the one which affects the value of unknown variable (x or y or z) of selection? They are the affecting the unknown variable, so we measure what is the factor with which they affect.
Points to note with respect to minors,
Known from minors,
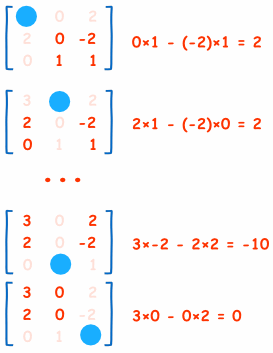
1. You can see we reject the row & column that falls inline with the unknown variables in below images and the consider the smaller matrix, 2x2 as minor.
2. This kind of selection clearly states that the values that are present inline with the unknown variables are not affecting the unknown variable.
Assumptions from my end from minors description, look to be true.
3. we rejected the row inline to variable/input, why? if we take the row, it represent the kernel function. It does not makes sense to state that input 1 is affecting input 2. We assumed the system to be linear. as we already clarified that inputs are independently affecting the system. you can apply x, then y and then z, or y, then x and then z, order does not matter.
4. we rejected the column inline to variable/input, why?The actual model is linear independent combination of x, y and z. x is the unknown under discussion, it can be affected by y and z only, not by itself. so the column inline is rejected.

3. The way Co-factors determined with minors can be +ve or -ve
it can be easily visualized, that there are +ve factors and -ve factors affecting the unknown.
[+ -
- +]

Factors are called as co-factors, as they come from different dimension. i.e., x is affected by y and z, y is affected by x and z etc.,
Vectors in the same direction affects +vely, and vectors in opposing direction affects -vely.

4. Why Adjunct is the transpose of Co-factor matrix?
Here is link questioning about the intuition of Adjunct.
https://math.stackexchange.com/questions/254774/what-is-the-intuitive-meaning-of-the-adjugate-matrix
1. Identity Matrix scaled by value of determinant is equal to Adj(A).A or A.Adj(A) is equals to I.Det(A) or Det(A).I
2. Adj(A) has same size or dimensions as A.
3. It is a natural pair of A.
It should exists for every invertible systems. i.e., x affecting y and z should be reversible. The impact should be translation and scaling only.
Adj(A) can be scaled by a common factor from A by 1/Det(A). if not scaled Det(A) is 1.
By Transpose, we change row to columns and columns to rows. When we balance the equations, we obvious multiply entire equation with common factor or cross multiply. We transpose Co-factor matrix and then multiply it Matrix A similar to Cross Multiply. Det(A) is the common factor, which is cancelled out post multiplication. We can also first divide by common factor and then cross multiply. If common factor is zero, there is no singular solution.
Like shown below,
To find 2/3 + 3/4, we multiply, first term with 4 and the second term with 3
(2*4) / (3*4) + (3*3)/(4*3) = 8/12 + 9/12
Now there is a common factor 12
So we can say
8/12 + 9/12 = (8+9)/12 = 17/12
Adj(A) is Transpose of Co-factor matrix.
Determinants says a lot of things about Matrices.
1. Says whether Matrix/system of equations is invertible or not.
By that, we question whether we can find x, y, z at all. A system has to be invertible if we have to determine it model with the help of inputs and outputs alone.
<To Include system and signals>
2. It deals with square matrix of all orders.
What are determinants?
Determinants are Tool to plots few points on graph
Determinant function is a tool to plot of more points on a graph, while we have already plotted few points saying these were empirical outcomes of the black box system.
Here det(A) is a number and A is a Matrix.
Quote from book,
In this chapter we will study “determinants” or, more precisely, “determinant functions.”Matrix is a Womb, as it is the container of determinant. Determinants are used to determine the properties of the function.
Unlike real-valued functions, such as f(x) = x^2 , that assign a real number to a real
variable x, determinant functions f(A) assign a real number to a matrix variable A.
Quote from book,
The term determinant was first introduced by the German mathematician Carl Friedrich
Gauss in 1801 (see p. 15), who used them to “determine” properties of certain kinds of functions. Interestingly, the term matrix is derived from a Latin word for “womb” because it was viewed as a container of determinants.
Determinants are Ratio of increase of the volume
There are lot of terms introduced in the below video like monte carlo integration, eigen values and eigen vectors, but the video completes with idea of determinants as below.
det(A) = increase volume / old volume
It confirms that that it is a scaling factor of all dimension. Whether it is scaling all dimension uniformly, is another question, you might wonder. Scaling may not be uniform, it could get skewed unless there are few characteristic vectors or eigen vectors.
If there are vectors that only stretch and don't change direction and their scaling is determined by some called as eigen values, then determinants can be easily expressed interms of eigen values over eigen vectors.
Determinants are Ratio of increase of the Area
In 3Blue1Brown channel, Determinant are stated as Ratio of increase of Area as they are not dealing with cube rather are dealing with 2x2 matrix and plane.
Geometrical Viewpoint of Vectors & Matrices
In almost in the entire play list, the matrices are treated as Vectors with origin at zero and the operation we do on vectors as Transformation, transformation can be like reflection, rotation, scaling over the basis etc., and the basis need not be co-ordinate system, rather i could be anything other than that, which is linearly translated or scaled. Any transformation taking place in basis also takes place on the entire system build on top of basis. Basis also determines the span of the system, i.e., all possible vectors on space given the basis.
Matrix is build with 2 or more vectors. Matrix multiplication is nothing but transformation on 2 or more vectors basis. It could be rotation, sheering or sometimes combination of both.
Inverse is nothing but reversal of the transformation to put back the basis vector in the place where it was present originally.
Basis vector is linearly dependent then its actual dimensions gets reduced and cannot be called as linearly independent or used for linear algebra.
Methods for Calculation of Determinants:
1. Cofactor Expansion
2. Condensation
References
https://www.ams.org/notices/199906/fea-bressoud.pdf
https://en.wikipedia.org/wiki/Dodgson_condensation
https://sms.math.nus.edu.sg/smsmedley/Vol-13-2/Some%20remarks%20on%20the%20history%20of%20linear%20algebra(CT%20Chong).pdf
https://docs.google.com/presentation/d/1qNj3lwCxLOELPfOIA735Phnr6fOp-v2Xk043pv3SHM0/edit#slide=id.p28
http://www.macs.citadel.edu/chenm/240.dir/12fal.dir/history2.pdf
http://courses.daiict.ac.in/pluginfile.php/15708/mod_resource/content/1/linear_algebra_History_Linear_Algebra.pdf


No comments:
Post a Comment