Reason for listing them down is for every methods in ADT as it difference from structure to structure and we have check runtime performance.
The way performance is calculated is based on inputs or sometime based on internal properties like height, depth, degree etc., But all the performance dependent on the Representation or implementation details (like graph / tree using vector, array, list etc.,)
Data Structures like Stack, Queues, Linked Lists, Tree, Graph are called as Abstract Data Types with few behaviors or operations or methods.
They are very special because, one has to know them before implementing any algorithm with them in advanced algorihtms where we don't make use of exact data structures provided out of box from programming languages but we will design them for our custom purposes with tweaks.
1. Stack - push, pop (INSERT and REMOVE, no traversal)
REPRESENTATION - ARRAY (BEST), LINKED LIST
2. Queue - enqueue, dequeue (INSERT and REMOVE, no traversal)
REPRESENTATION - ARRAY (BEST), LINKED LIST
3. Linked list - first, last, before, after (Traversal is like a person climbing a rope)
Insert for Singly linked list alone is a special case, it take much time when compared to doubly linked list. (It is not a chain where we could de-link and link anywhere, every time one has to traverse from first)
உலகப் புகழ் பெற்ற ஜெர்மானியக் கணித அறிஞர் ஹெர்மான் மின்கோவ்ஸ்கி (Hermann Minkowski) பிறந்த தினம் - சூன் 22:
ரஷ்யப் பேரரசின் ஒரு பகுதியாக இருந்த போலந்தில் அலெக்சோட்டாஸ் என்ற சிற்றூரில் யூதக் குடும்பத்தில் பிறந்தார் (1864). தந்தை, வர்த்தகர். 7 வயதுவரை வீட்டிலேயே கல்வி கற்றார். 1872-ல் குடும்பம் ஜெர்மனியில் குடியேறியது. கல்வியைத் தொடர்வதற்காக பிராடஸ்டென்டாக மதம் மாறினார்.
15-வது வயதில் ஜெர்மனியில் உள்ள அல்பெர்டினா கோனிக்ஸ்பெர்க் பல்கலைக்கழகத்தில் பயின்றார். பின்னர் பெர்லின் பல்கலைக்கழகத்தில் சேர்ந்தார், கணிதத்தின் இருபடிவ வடிவில் (quadratic forms) ஆர்வம் கொண்டு அதுகுறித்து ஆராய்ந்தார். இங்கு படித்துக் கொண்டிருந்தபோதே 18 வயதில் பிரெஞ்ச் அறிவியல் அகாடமியின் கணிதவியல் பரிசை வென்றவர்.
அப்போது ஒருங்கிணைந்த குணகங்களுடன் (integral coefficients) n மாறிலிகள் உள்ள இருபடி வடிவங்கள் குறித்து 140 பக்கங்கள் கொண்ட நிபுணத்துவம் வாய்ந்த கட்டுரையை எழுதினார். இளங்கலை, முதுகலைப் பட்டப் படிப்பு முடிந்தபின் 1885-ல் முனைவர் பட்டம் பெற்றார்.
மின்னியக்க விசையியல் குறித்து அறிந்து கொள்வதற்காக அதற்கான கருத்தரங்குகளில் பங்கேற்றார். முதலில் பான் பல்கலைக்கழகத்தில் ஆசிரியராகப் பணியாற்றினார். பின்னர் துணைப் பேராசிரியராக உயர்ந்தார்.
கணித இயற்பியலின் ஒரு பகுதியான கச்சிதமான திரவத்தில் (perfect liquid) மூழ்கிய திடப்பொருள்களின் இயக்கம் குறித்து ஆய்வுகள் மேற்கொண்டார். கோட்டிங்கன், கோனிக்ஸ்பெர்க் மற்றும் சூரிச் பல்கலைக்கழகங்களில் பொறியியல் மற்றும் கணித ஆசிரியராகப் பணியாற்றினார்.
சூரிச்சில் உள்ள பாலிடெக்னிக்கில் ஆசிரியராக இருந்த சமயத்தில் இவரது மாணவர்களில் ஐன்ஸ்டீன், கான்ஸ்டன்டின் கார்தோடோரி ஆகியோர் குறிப்பிடத்தக்கவர்கள். இருபடிவ வடிவங்களைக் குறித்து ஆராய்ந்தார். எண் கோட்பாட்டுச் சிக்கல்களை வடிவியல் முறைகளைக் கொண்டு தீர்வு காணும் எண்களின் வடிவியல் என்ற கோட்பாட்டைக் கண்டறிந்து வெளியிட்டார்.
கோட்டிங்கன் பல்கலைக்கழகத்தில் 1902-ம் ஆண்டு தலைமைப் பொறுப்பேற்ற இவர், இறுதிவரை அங்கு பணியாற்றினார். கணித எண்களின் வடிவியல் முறையை நிரூபணம் செய்து மேம்படுத்தினார். மேலும் எண் கோட்பாடு, கணித இயற்பியல், சார்பியல் கோட்பாடு உள்ளிட்டவைகளுக்கு கணிதத் தீர்க்க வடிவியல் முறைகளைப் பயன்படுத்தினார்.
இவரது எண்களின் வடிவியல் கோட்பாடுகள், செயல்பாட்டுப் பகுப்பாய்விலும் டைபோண்டின் தோராயத்திலும் (approximation) பயன்படுத்தப்படுகின்றன. மேலும் வடிவியல் கோட்பாடு மூலம் எண் கோட்பாட்டுக் கணிதங்களுக்குத் தீர்வுகளை வழங்கினார். தனது ஆராய்ச்சிகளையும் கண்டுபிடிப்புகளையும் அவ்வப்போது கட்டுரைகளாக எழுதி வெளியிட்டு வந்தார்.
இவை அனைத்தும் இவரது நண்பர்களால் தொகுக்கப்பட்டு ‘கலெக்டட் பேப்பர்ஸ்’ என்ற தலைப்பில் நூலாக வெளியிடப்பட்டது. ‘ஸ்பேஸ் அன்ட் டைம்’ என்ற இவரது நூல் மிக முக்கியமான படைப்பாகப் புகழ்பெற்றது. ஐன்ஸ்டீனின் சார்பியல் கோட்பாட்டுக்கான கணித அடித்தளத்தை அமைத்தவர்.
நாற்பரிமாண மின்கோவ்ஸ்கி வெளி - நேரம் (Minkowski space) கோட்பாட்டைக் கண்டறிந்தவர். நவீன கணித மேம்பாட்டுக்கு இவரது ஆய்வுகள் பெரிதும் உதவின. குறுகிய வாழ்நாளில் கணித இயற்பியல், சார்பியல் கோட்பாடு உள்ளிட்ட பல்வேறு களங்களில் குறிப்பிடத்தக்கப் பங்களிப்புகளை வழங்கிய கணிதமேதை ஹெர்மான் மின்கோவ்ஸ்கி 1909-ம் ஆண்டு மறைந்தார்.
our correlation problem the professor said that the null hypothesis was that they are not correlated .. so if we chose the null hypothesis as ‘Related’ then the same data set will prove that they are not related. What decides what is to be chosen as a null hypothesis ?
Student 2:
As far I read and understood Null hypothesis should be an evenly or normally applicable cases which obeys guassian bell shaped population distribution curve, z and t distribution and highly probable. With tests like F-test, chi square test, ANOVA based on type of data and significance factor, we always like to disprove null hypothesis to state that we discovered something which is not NORMAL, to claim EUREKA moment. If we fail we will say we failed to reject null hypothesis rather saying NULL hypothesis got proved or won.
Considering the professor answer, he says that the data is already "not related" in general sense and it is under the bell shaped distribution population. Anyway we will fail to reject NULL hypothesis, if we take "not relating" as NULL hypothesis.
Taking the data as "related" as our NULL hypothesis does not make any sense if that is not the highly probable happening and falling under bell shaped curve or distribution so we could disprove and say we discovered something against it.
Student 3:
Null Hypothesis by definition states that there is no relation between the compared fields. So you can't choose the null hypothesis as "related".
For example the field "Employee ID" will most likely have no relation to the field "COVID Positive". So if we were to compare the chi-square of the 2, you'll see it fall below the required value, which would mean that null hypothesis is valid and thus you can ignore the field
Takeaways,
1. Determinant is nothing but a Common multiple factor or Scaling factor by which all the dimension have increased/reduced in its area, volume etc.,
2. Adjugate Matrix multiplication with Matrix is like Cross Multiplication.
3. Inverse of A is division by Common factor and Cross multiplication of transpose of co-factor Matrix of A.
4. Transpose of co-factors are only named as Adjugate - this naming is leading to all cause of confusion.
The use of the term adjoint for the transpose of the matrix of cofactors appears to have been introduced by the American mathematician L. E. Dickson in a research paper that he published in 1902.
5. Ways to calculate Determinants.
6. Theorems on Determinants.
|A| = det(A) ≠ 0. A matrix is said to be invertible, non-singular, or non–degenerative.
I tried to explain determinant and adjuncts, but was fairly unsuccessful with my previous blog. With this blog, i like to give a one more try.
I lost my flow, when i started explaining, minor, co-factors and failed to explain why determination is manipulated with minors and how the sign of co-factors play a role in the calculation towards the single value Determinant.
Blogging this stuff is not going to help my M.Tech in data science but will help to gain deeper insight to gain better intuition.
My Book for references is "Elementary Linear Algebra by Howard Anton / Chris Rorrers", I am sure google gave me this book as the best for learning linear algebra few months back.
It has a chapter for deteminants with 3 subsections.
1. Determinats by co-factor expansion.
2. Evaluating deteminant by Row Reduction.
3. Properties of Deteminants; Cramers Rule.
Few of my assumptions:
1. black box under study and the kernels
What is Black Box?
Consider a simple system of equations,
x+y+z = 25
2x+3y+4z = 120
5x+3y+z = 30
we can call x, y, z as 3 inputs, we don't know the exact system. The system to which we send the inputs was a black box. We got the output as 25. one of our empirical formula to describe black box is linear combination of all three inputs which is x+y+z. As far now the kernel of the system is x+y+z =25.
Similarly we have 2 more kernel of the same system 2x+3y+4z = 120 and 5x+3y+z = 30. With these three kernel, we try to determine actual system model.
Model is mathematical model, once we identify this, we know for any input of x, y, z what will be the value of b. That is we could calculate output of 4x+6y+7z. which we don't know.
Model is our Black Box.
What is kernel?
Kernel in these languages are nothing but seed. It has got all information about the plant, the plant could be a vegetable plant, fruit plant or a banyan tree, anything at all. We don't know we have to figure out.
Kernel is nothing but any f(x) function. Here we have 3 variable, so it is f(x,y,z), it maps to constant value some "b" as output. We don't know what is f function. But we know f(x,y,z) = b or AX=B as we assumed our system to be linear. X =(x,y,z) vector, A is the matrix f, as we don't deal with one kernel but 3. B is b, but it is a vector.
vector is nothing but a tuple, but it is a special tuple as it is formed from three independent observation or empirical outcomes and they are pointing the direction for us for finding actual model / black box.
2. Minors are subsets, affecting factors of the unknown variables/inputs x, y, z
Minors are the one which affects the value of unknown variable (x or y or z) of selection? They are the affecting the unknown variable, so we measure what is the factor with which they affect.
Points to note with respect to minors,
Known from minors,
1. You can see we reject the row & column that falls inline with the unknown variables in below images and the consider the smaller matrix, 2x2 as minor.
2. This kind of selection clearly states that the values that are present inline with the unknown variables are not affecting the unknown variable.
Assumptions from my end from minors description, look to be true.
3. we rejected the row inline to variable/input, why? if we take the row, it represent the kernel function. It does not makes sense to state that input 1 is affecting input 2. We assumed the system to be linear. as we already clarified that inputs are independently affecting the system. you can apply x, then y and then z, or y, then x and then z, order does not matter.
4. we rejected the column inline to variable/input, why?The actual model is linear independent combination of x, y and z. x is the unknown under discussion, it can be affected by y and z only, not by itself. so the column inline is rejected.
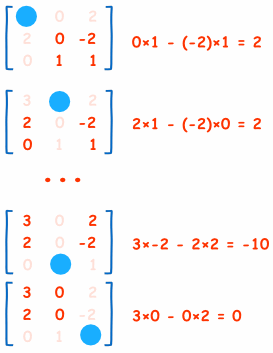
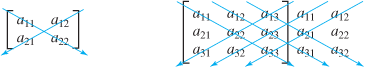
3. The way Co-factors determined with minors can be +ve or -ve
it can be easily visualized, that there are +ve factors and -ve factors affecting the unknown.
[+ -
- +]
Factors are called as co-factors, as they come from different dimension. i.e., x is affected by y and z, y is affected by x and z etc.,
Vectors in the same direction affects +vely, and vectors in opposing direction affects -vely.
4. Why Adjunct is the transpose of Co-factor matrix?
1. Identity Matrix scaled by value of determinant is equal to Adj(A).A or A.Adj(A) is equals to I.Det(A) or Det(A).I
2. Adj(A) has same size or dimensions as A.
3. It is a natural pair of A.
It should exists for every invertible systems. i.e., x affecting y and z should be reversible. The impact should be translation and scaling only.
Adj(A) can be scaled by a common factor from A by 1/Det(A). if not scaled Det(A) is 1.
By Transpose, we change row to columns and columns to rows. When we balance the equations, we obvious multiply entire equation with common factor or cross multiply. We transpose Co-factor matrix and then multiply it Matrix A similar to Cross Multiply. Det(A) is the common factor, which is cancelled out post multiplication. We can also first divide by common factor and then cross multiply. If common factor is zero, there is no singular solution.
Like shown below,
To find 2/3 + 3/4, we multiply, first term with 4 and the second term with 3
(2*4) / (3*4) + (3*3)/(4*3) = 8/12 + 9/12
Now there is a common factor 12
So we can say
8/12 + 9/12 = (8+9)/12 = 17/12
Adj(A) is Transpose of Co-factor matrix.
Determinants says a lot of things about Matrices.
1. Says whether Matrix/system of equations is invertible or not.
By that, we question whether we can find x, y, z at all. A system has to be invertible if we have to determine it model with the help of inputs and outputs alone.
<To Include system and signals>
2. It deals with square matrix of all orders.
What are determinants?
Determinants are Tool to plots few points on graph
Determinant function is a tool to plot of more points on a graph, while we have already plotted few points saying these were empirical outcomes of the black box system.
Here det(A) is a number and A is a Matrix.
Quote from book,
In this chapter we will study “determinants” or, more precisely, “determinant functions.”
Unlike real-valued functions, such as f(x) = x^2 , that assign a real number to a real
variable x, determinant functions f(A) assign a real number to a matrix variable A.
Matrix is a Womb, as it is the container of determinant. Determinants are used to determine the properties of the function.
Quote from book,
The term determinant was first introduced by the German mathematician Carl Friedrich
Gauss in 1801 (see p. 15), who used them to “determine” properties of certain kinds of functions. Interestingly, the term matrix is derived from a Latin word for “womb” because it was viewed as a container of determinants.
Determinants are Ratio of increase of the volume
There are lot of terms introduced in the below video like monte carlo integration, eigen values and eigen vectors, but the video completes with idea of determinants as below.
det(A) = increase volume / old volume
It confirms that that it is a scaling factor of all dimension. Whether it is scaling all dimension uniformly, is another question, you might wonder. Scaling may not be uniform, it could get skewed unless there are few characteristic vectors or eigen vectors.
If there are vectors that only stretch and don't change direction and their scaling is determined by some called as eigen values, then determinants can be easily expressed interms of eigen values over eigen vectors.
Determinants are Ratio of increase of the Area
In 3Blue1Brown channel, Determinant are stated as Ratio of increase of Area as they are not dealing with cube rather are dealing with 2x2 matrix and plane.
Geometrical Viewpoint of Vectors & Matrices
In almost in the entire play list, the matrices are treated as Vectors with origin at zero and the operation we do on vectors as Transformation, transformation can be like reflection, rotation, scaling over the basis etc., and the basis need not be co-ordinate system, rather i could be anything other than that, which is linearly translated or scaled. Any transformation taking place in basis also takes place on the entire system build on top of basis. Basis also determines the span of the system, i.e., all possible vectors on space given the basis.
Matrix is build with 2 or more vectors. Matrix multiplication is nothing but transformation on 2 or more vectors basis. It could be rotation, sheering or sometimes combination of both.
Inverse is nothing but reversal of the transformation to put back the basis vector in the place where it was present originally.
Basis vector is linearly dependent then its actual dimensions gets reduced and cannot be called as linearly independent or used for linear algebra.
I have been hearing the song "asai mugam maranthu po che" many times, I thought it was a song on Kannan (lord krishna), recently based on the comments on the video, I found that this song is written by Subramaniya Bharathiyar. The reality of why he wrote this did touch heart too deep. Bharathiyar has written many songs with deep meanings despite looking naive.
Below is a verses from bharathi, which everyone must seek day in and day out. Every line is a gem. Clearly shows how much understanding he had about life. I love this word திண்ணிய நெஞ்சம், it emphasizes to make rooms for everyone in our life, which I do strive to achieve.
எண்ணிய முடிதல் வேண்டும், நல்லவே யெண்ணல் வேண்டும்; திண்ணிய நெஞ்சம் வேண்டும், தெளிந்த நல் லறிவு வேண்டும்; பண்ணிய பாவமெல்லாம் பரிதி முன் பனியே போல, நண்ணிய நின்மு னிங்கு நசித்திட வேண்டும் அன்னாய்!
Below is the song, i enjoy and the comment I told you.
This great song was written by an awesome Tamil poet "Subramaniya Bharathiyar'. It seems after he lost his one and only dear mother, he had a photograph of her to remind her. He somehow lost that photo as well and he was shaken by grief. Thus this song.Aasaimugam marantho pochey,Oh! I have forgotten my dear love's face my friendidhai Yaaridam solven adi thozhi;I don't know to whom I must address this complaintNesam marakavillai nenjam,the heart though has not forgotten its fondnessenil Ninaivu mugam marakalaamo;then how could my memories let me down? Kannil theriyuthoru thotram,The form that I perceiveathil Kannan azhagu muzhuthillaihas not in sum all his beautyNannu mugavadivu kaanil, andhaIn those eyes set in that beauteous visageNallavalla sirippai kaanom;I find not his sweet winsome smileOivu mozhithalum illamalwithout any respiteAvan uravai ninaithirukkum ullammy heart dwells on our relationshipvayum uraipathundu kandaiYou would notice thatAndha maayan pughazhinai eppodumI constantly speak that illusionist's praise alwaysKangal purinthuvitta paavamBut a sin committed by my eyesuyir Kannan urumarakkalachuhas caused his disappearance from sightpengalinidathil idu polehave you noticed such follyoru pedamai munbu kandathundo?In other women my friend?Thenai maranthirukkum vandumCan you ever find a bee that forsakes honeyoli sirappai maranthuvitta poovumA flower that shirks sunlightvaanai maranthirukkum payiruma crop that ignores rainIndha vaiyam muzhuthumillai thozhiany place else in this world?Kannan mugam maranthuponal,If I could forget Kannan's faceintha Kangal irunthu payan undo;Could I have further use for these eyes?Vanna padamumillai kandai,Alas! I don't even have a colourful picture of hisinni Vaazhum vazhi ennadi thozhi;How do I live out the rest of my life in this state my friend?
Sometimes, life may seem simply stressful. To cope with the
sometimes overwhelming nature of work or daily routines, it’s good to have a
go-to strategy to help you unwind when you’ve had a particularly taxing day or
week.
When the
day or week gets to be too much, what is your preferred method of unplugging
and recharging?
When it all
seems to be too much, take a step back, breathe, and try out one of these
techniques.
1. Heading Outdoors
The best
way to unplug and recharge is to head out to a natural spot away from the
bustle of the city. You can either take a walk in a park nearby or camp out if
you can. Spending some time in nature can help you relax completely so that
you’re energized when it’s time to return to work.
2. Pursuing a Hobby
It’s
helpful to have a hobby that lets you disconnect from work completely. Taking a
few hours to do pottery, read, or woodwork can give your mind a much-needed
break by distracting it. After spending some time working with your hands and
occupying your mind, you should find yourself refreshed with new ideas or a
renewed willingness to work.
3. Spending Time With
Family
When I’m
not working or having a particularly stressful day, I make sure that I spend
some extra time with my family. Generally, we don’t browse on our phones, check
emails, or text while we are spending time together. Staying close to my family
keeps me mentally strong and ready to overcome the challenges that arise in my
industry and business. –
4. Reading
Reading
takes you to another place and, for me, is the perfect way to unwind after a
long day. I spend my workday staring at a screen constantly, and the change of
pace is super important to give my eyes and body a rest. –
5. Meditation
Meditation
gets you out of your head and clears your mind so you’re prepared for anything
that lies ahead. It reduces stress and refreshes your mind so you’re mentally
prepared to tackle your to-do list and succeed.
6. Catching Up on the
News
When the
day gets to be too much, I like to take a break and catch up on the news. It
can be industry news or just perusing the New York Times, but spending a few
minutes letting my brain switch gears into a more passive mode can be really
refreshing, and the end of an article is a great natural point to jump back
into the tasks at hand.
7. Listening to Music
I believe
most owners and founders are creatives who have some internal need to be
working on or creating something. Personally, I unplug and recharge by getting
my “creative fix” spending time working on something that I enjoy, which isn’t
connected to my professional life: music. Playing an instrument or working on a
composition is a great way to let your mind go in a completely different
direction.
8. Exercising
When I get
overwhelmed with the size of my to-do list and everything feels like too much,
I go for an extensive (but not too intense) workout. Whether it’s a
comprehensive weight lifting session or a long bike trip, it helps me get back
the momentum of getting things done, leaves me energized, and helps me keep my
mind off work for a while.
9. Singing Along With
Beyonce or a Retro Song
I love
music, folk, classical, hip-hop, rock, drum & bass because I find them so
motivating and inspiring. Every time I listen to music I sing along, dance, or
exercise with any of the songs, music and I finish happier and recharged. Tasks
are easier when music is played.
10. Swimming Laps
When things
get overwhelming, I make sure to prioritize getting out and doing something
physical. I find that swimming laps is a great way to disconnect. You can’t
answer emails or phone calls when you are in a pool. Whenever I prioritize
getting to the pool in the morning before work or after a long day in the
office, I walk away feeling more energized and less stressed.
11. Watching a Movie
It sounds
really simple, but I like to sit down and enjoy a movie with my family. When
you intentionally decided to do something relaxing and watch a story unfold, it
takes you out of the stress life can create. Sometimes it’s a funny movie and
we end laughing all night, or it might be an action or drama that really puts
your own problems and life into perspective.
12. Taking a Coffee
Break
When I feel
that the pressure during the day is getting a bit too much, I take a coffee
break with my team. In our company, coffee is like an intermission from
work/bonding/creative brainstorming thing. I’d say that coffee is almost a part
of our company culture. We even added it to the title of one of our YouTube
series.
13. Talking to Someone
Outside of Work
When I want
to recharge, it’s refreshing to talk to a friend or family member who’s not
connected to work or whatever I may be stressing about. Meeting for lunch, a
cup of coffee, or talking on the phone gives me another perspective and reminds
me that there’s a lot going on beyond my bubble.
14. Unplugging and
Diving Into Fiction
Reading
helps reduce my stress when I’m feeling overworked and pressured. I prefer to
read fiction because it’s easier for me to focus on exciting and otherworldly
adventures instead of fact-based true stories. The best part is I always feel
refreshed by the time I put it down. I think that unplugging and diving into a
book will help you overcome stressful days.
I was set in motion by one of the Math Assignment in Mathematics for data foundation course.
The question under consideration is whether we can do dimensional reduction? or not post SVD. What parameter and components should look out for post SVD analysis.
I started with this document - http://courses.cs.tamu.edu/rgutier/cs790_w02/l5.pdf. A PPT with good insight into error post PCA and clarifying that Dominant Eigen Value, and corresponding Eigen Vector to be considered for Dimensional Reduction.
I did not get the difference between 2 principle axis (highest spread axis & residual error axis), until I read the paper https://blog.paperspace.com/dimension-reduction-with-principal-component-analysis/
Apart from PCA, ICA and other Dimensional reduction techniques are revealing various dimensional worlds to me. They lead me until deep learning (autoencoders) with the related links in above paper.
I had been getting an hit related to Co-relation and SVD. The below paper clarified the relationship
SVD and PCA are linear analysis, I also got to know that Independent component means Independent both linearly and non linearly. (Note: Correlation only show linear relationships only, it does not compare non linear relationships)
There are lot of wonderful comprehensions of DIMENSIONAL REDUCTION and a lot to learn.
Below are the Summary of good links to browse through.
